Piano Tuners and the Explosion in Beirut

Fermi estimation might get you a job at Google, or help you identify nonsense news

At the time, I thought the questions were just ridiculous.

Every exam contained one problem that had nothing at all to do with first-year college chemistry. They came completely out of nowhere, like a piano falling from the sky. Or a piano tuner.

“How many piano tuners are there in New York City?” That’s the one I remember most vividly.

My thought process went approximately like this: No fair! WTF is this?? I have no idea… 10,000?

I was very wrong with that answer. In retrospect, I was very wrong about the question, too. Far from ridiculous, that question and others like it led to one of the most useful lessons I have ever learned in a classroom.

The questions were examples of so-called “Fermi problems.” Enrico Fermi—who created the first nuclear reactor beneath the University of Chicago football field—often made (and asked others to make) back-of-the-envelope estimates to help approach problems. (Fermi famously did this to estimate the strength of the first atomic explosion.) Part of his lesson was that a certain mental strategy is often more important for attacking a problem than is detailed prior knowledge. The strategy entails breaking the problem down into many pieces and making estimates for each one; none of the estimates has to be particularly accurate for the end result to be sensible. Here’s how I should have addressed the piano tuners:

—How many people do I think live in New York City? About 9 million.

—How many people are in the average household? Let’s say three. So 3 million households.

—What portion of households do I think have a piano? Not really sure…some Upper East Siders probably have two, but let’s say one in ten overall. So 300,000 pianos.

—How often is a piano tuned? I certainly don’t know, but sounds like an annual thing, or at least in that ballpark.

—How many pianos can one tuner service in a day? Hmmm…let’s say an hour per piano, plus transit and breaks and all that, so let’s say five per day.

—How many days does a piano tuner work? There are about 260 weekdays in a year, minus a few weeks of holidays, so say 240 workdays, which would mean that one piano tuner can tune about 1,200 pianos a year. So 300,000 pianos divided by 1,200 pianos-per-tuner-per-year means we need 250 piano tuners to keep NYC in tune.

Now what’s the actual answer? I don’t know exactly—I just redid that in real time with a series of guesses, as I should have the first time around—but I’m pretty sure I got the right order of magnitude. According to WIRED, Google has used “How many piano tuners are there in Chicago?” as a question in job interviews. WIRED reported that the Yellow Pages lists 83 tuners in Chicago, with a few duplicates, so WIRED thinks about 60. I prefer to stick with 83, because New York City has about three times the population of Chicago, and 83 x 3 is 249, so that’s more favorable to my estimate. (Future Range Report topic: confirmation bias!)

I don’t know anything about piano tuning, but using the Fermi strategy I could easily have realized that my 10,000 answer was nonsensical. More importantly, understanding and practicing Fermi estimation ultimately became one of the most useful tools in my cognitive garage. I use Fermi estimation constantly to consider whether news articles and academic papers even make sense on their face before I bother to dive deeper; some of my articles and parts of my books were born when Fermi estimation helped me realize that certain scientific papers or popular news articles made no sense and couldn’t possibly be accurate.

In chapter two of Range, I talk a bit about Fermi estimation, and mention that it’s one of the topics in the University of Washington course INFO 198/BIOL 106B, or, by its more popular name: “Calling Bullshit.” The instructors use a news case study to demonstrate “how Fermi estimation can cut through bullshit like a hot knife through butter.”

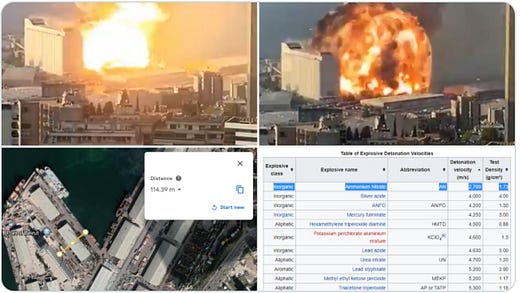
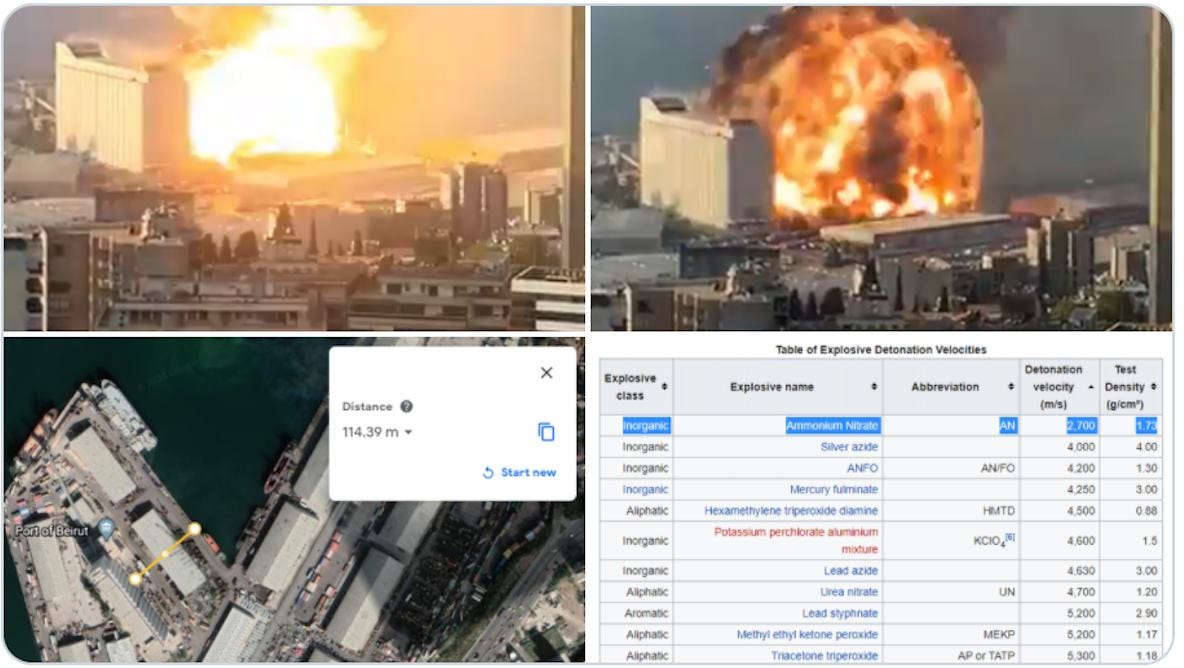
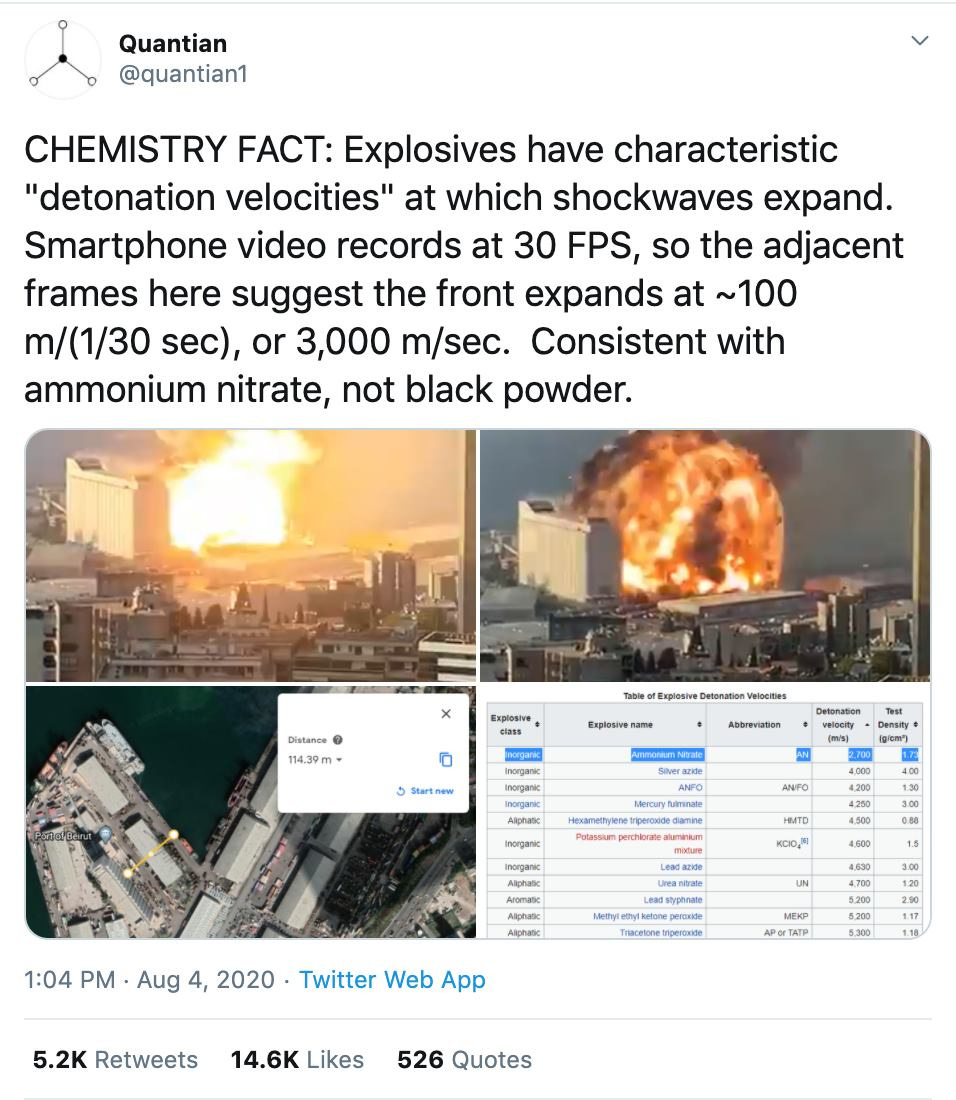
Last week, I saw an important example of Fermi estimation in the wake of the horrendous explosion in Beirut. I first learned of the explosion on Twitter when my timeline filled up with authoritative descriptions alleging various explosive materials and photographs with red circles around some dot in the sky that the Twitter user claimed was a missile or fighter plane. Some tweeters were arguing about the recent political motivations of several countries—their attempt to demonstrate that it was most likely an attack. And then I came across this tweet below:

This Twitter user combined still shots from a widely available video, the frame rate of smartphone cameras, a quick Google Earth search, and a Wikipedia list of the detonation velocities of different materials to show that the Beirut explosion was definitely not gunpowder, and was consistent with the fertilizer ammonium nitrate, which turned out to be the case. That’s a more sophisticated Fermi estimation than my piano tuners example, but it’s a similar approach, and used widely available tools rather than any particular prior knowledge. That’s an impressive example of calling bullshit.

Most of the time I use Fermi estimation, I don’t even have to get a correct answer like that Twitter user did; I’m just trying to determine if someone else’s conclusion is implausible. So here’s my tip: practice! You get a lot better at Fermi estimation by practicing. Unsurprisingly, the superforecasters I wrote about in Range—and who are making “eerily accurate” Covid-19 predictions—tend to use Fermi estimation a lot.

Start simple and easily searchable: How many heartbeats are in an average human life? How many periods are in a Harry Potter book? Break it down, and try to get the right order of magnitude… But, in general, just be number-curious when you read the news. Next time you see a report about new Covid-19 cases in some city, try to guess the population of that city (if you don’t already know it), and then the population of the state, and then how many miles it is away from you. And then, when you get more advanced, what proportion of that state is farmland.

It’s not easy at first, and if you don’t get a few wildly wrong, then they aren’t hard enough. (Desirable difficulties, people! You should be wrong at least 15 percent of the time on anything you practice.) But if you practice, pretty quickly you’ll get better, and you’ll get oriented to estimating in a way that I’ve found incredibly helpful. Soon you’ll even be calling your own bullshit, like I did with the piano tuners…only too late for my chemistry exam. Sigh.

Thanks so much for reading. Until next time….

David